Notiuni

Definiţie. Gradul unui vârf x este numărul muchiilor incidente cu x.
Gradul vârfului x se notează cu d(x).
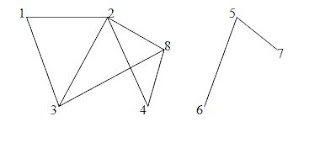
Ex. în Fig.1 d(1)=3, d(4)=2, d(8)=0, d(6)=1
Un vârf care are gradul 0 se numeşte vârf izolat.
Un vârf care are gradul 1 se numeşte vârf terminal.
Propoziţia 1. Dacă un graf G=(X,U) are m muchii şi n vârfuri iar X={x1,x2,..,xn}, atunci d(x1)+d(x2)+...+d(xn)=2m.
Corolar. În orice graf G există un număr par de vârfuri de grad impar.
Definiţie. Se numeşte graf complet cu n vârfuri un graf care are proprietatea că orice două noduri diferite sunt adiacente.
Propoziţia 2. Un graf complet Kn are n(n-1)/2 muchii.
Definiţie. Un graf G=(X,U) se numeşte bipartit dacă există două mulţimi nevide A, B astfel încât X=A U B, A Ç B =F şi orice muchie u a lui G are o extremitate în A iar cealaltă în B.
Definiţie. Un graf bipartit se numeşte complet dacă pentru orice x din A şi orice y din B, există în G muchia [x,y].

Definiţie. Se numeşte lanţ în G succesiunea de vârfuri L={xi1, xi2,..., xik} cu proprietatea că orice două noduri consecutive din L sunt adiacente, adică [xi1, xi2], [xi2, xi3],..., [xik-1, xik] Î U.
Dacă vârfurile xi1, xi2,..., xik sunt diferite două câte două atunci lanţul se numeşte elementar. În caz contrar, lanţul este neelementar.